We say an \((n,n)\)-function \(F \colon \mathbb{F}_2^n \to \mathbb{F}_2^n\) is a crooked function if for any nonzero \(a \in \mathbb{F}_2^n\), the image of \(D_aF(x)=F(x)+F(x+a)\) is an affine hyperplane. The only known examples of crooked functions are all quadratic almost perfect nonlinear (APN), or equivalently, for every known crooked function, \(D_aF\) is affine for all \(a \in \mathbb{F}_2^n\). The ortho-derivative \(\pi_F \colon\mathbb{F}_2^n \to \mathbb{F}_2^n\) of a crooked function \(F\) is the function such that \(\pi_F(0)=0\), and for any nonzero \(a\), the set \(\{0,\pi_F(a)\}^\perp\) is the underlying vector space of \(\mathrm{Im}(D_aF)\). We prove that for \(n \geq 4\) and a crooked function \(F\), if \(k\) is a non-negative integer such that \(F\) has \(2^k\) quadratic component functions, \(\pi_F\) has at least \(2^n-2^{n-k}\) nonzero components of algebraic degree \(n-2\). In particular, we resolve Gorodilova's conjecture that every nonzero component of \(\pi_F\) has algebraic degree \(n-2\) when \(F\) is quadratic APN. As a corollary, we prove that for any even \(n \geq 4\), any crooked \((n,n)\)-function with at least one quadratic component has at least \(5\) semi-bent components. As a second main result, for \(n \geq 4\), we associate to a crooked function \(F\) a quadratic function \(\varepsilon_F \colon \mathbb{F}_2^n \to \mathbb{F}_2^n\) that satisfies a strong geometric-combinatorial condition regarding the sums of \(F\) over \(2\)-dimensional linear subspaces. Furthermore, we obtain a congruence result on a problem on \(m\)-sequences introduced by Johansen, Helleseth, and Kholosha, and we determine the exact algebraic degrees of some Boolean functions associated to the bent and near-bent components of particular classes of plateaued vectorial functions.

Quadratic Boolean functions (that is, Boolean functions of algebraic degree at most 2), bent Boolean functions (i.e. maximally nonlinear Boolean functions in even numbers of variables) and, as we prove in this paper, partially-bent Boolean functions (i.e. affine extensions of bent functions to linear super-spaces), share a strong property: all their restrictions to affine hyperplanes are plateaued (i.e. have a Walsh transform valued in a set of the form \(\{0,\pm \lambda\}\), where \(\lambda\) is a positive integer called the amplitude). In this paper we determine for any \(n\) and \(k< n\) the class \(C^n_k\) of those \(n\)-variable Boolean functions whose restrictions to all \(k\)-dimensional affine subspaces of \(\mathbb{F}_2^n\) are plateaued (of any amplitude). We characterize partially-bent (resp., quadratic) Boolean functions as those functions that are plateaued on any affine hyperplane (resp., any affine subspace of dimension \(k\), where \(3 \leq k \leq n-2\), while these are all Boolean functions for \(0\leq k\leq 2\)). For \(n\geq 5\), each of the following classes of Boolean functions happens then to be strictly included in the next one: quadratic functions, partially-bent functions, the restrictions of partially-bent functions to affine hyperplanes, plateaued functions, the restrictions of plateaued functions to affine hyperplanes, and all Boolean functions. We leave open the two problems of determining exactly what are the third and fifth of these classes (we begin the study of the first of these two classes by giving a non-trivial characterization). Our characterization of partially-bent (resp., quadratic) functions extends to strongly plateaued vectorial functions. We state an open question on vectorial functions that happens to be related to an important one on crooked functions.

Whether two distinct APN functions can have a Hamming distance of \(1\) remains an open problem. In 2020, L. Budaghyan et al. introduced a new CCZ-invariant \(\Pi_F\) which can be used to provide lower bounds on the Hamming distance between a given APN function \(F \colon \mathbb{F}_2^n \to \mathbb{F}_2^n\) and other APN functions. Lower bounds on the distance from an APN function \(F\) to any other APN function \(G\) are known when \(F\) is an almost bent (AB) function or when \(F\) is a \(3\)-to-\(1\) quadratic function with \(n\) even. In this paper, we reinterpret \(\Pi_F\) in terms of the multiplicities of the 3-sums of the graph \(\mathcal{G}_F=\{(x, F(x)) : x \in \mathbb{F}_2^n\}\) of \(F\) as a Sidon set, which we call exclude multiplicities. For even \(n\), we establish lower bounds on the distance between \(F\) and any other APN function \(G\) when \(F\) is plateaued APN, and we generalize a previously known lower bound for quadratic \(3\)-to-\(1\) functions to the case where \(F\) is plateaued \(3\)-to-\(1\) (e.g., when \(F\) is a Kasami function). For odd \(n\), we derive new lower bounds when \(F\) is the APN inverse function over \(\mathbb{F}_{2^n}\). We also study how the exclude multiplicities of \(\mathcal{G}_F\) are directly connected to the existence of linear structures of \(\gamma_F\) when \(F\) is plateaued APN and to the ortho-derivative when \(F\) is a quadratic APN function. In particular, we prove that \(\gamma_F\) has no nontrivial linear structures when \(F\) is plateaued APN. We also use the CCZ-invariance of exclude multiplicities to prove that the Brinkmann-Leander-Edel-Pott function is not CCZ-equivalent to a plateaued function.

A Sidon set \(S\) in \(\mathbb{F}_2^n\) is a set such that \(x+y=z+w\) has no solutions \(x,y,z,w \in S\) with \(x,y,z,w\) all distinct. In this paper, we prove various results on Sidon sets by using or generalizing known cryptographic results. In particular, we generalize known results on the Walsh transform of almost perfect nonlinear (APN) functions to Sidon sets. One such result is that we classify Sidon sets with minimal linearity as those that are \(k\)-covers. That is, Sidon sets with minimal linearity are those Sidon sets \(S \subseteq \mathbb{F}_2^n\) such that there exists \(k > 0\) such that for any \(p \in \mathbb{F}_2^n \setminus S\), there are exactly \(k\) subsets \(\{x,y,z\} \subseteq S\) such that \(x+y+z = p\). From this, we also classify \(k\)-covers by means of the Cayley graph of a particular Boolean function, and we construct the unique rank \(3\) strongly regular graph with parameters \((2048, 276, 44, 36)\) as the Cayley graph of a Boolean function. Finally, by computing the linearity of a particular family of Sidon sets, we increase the best-known lower bound of the largest Sidon set in \(\mathbb{F}_2^{4t+1}\) by \(1\) for all \(t \geq 4\).

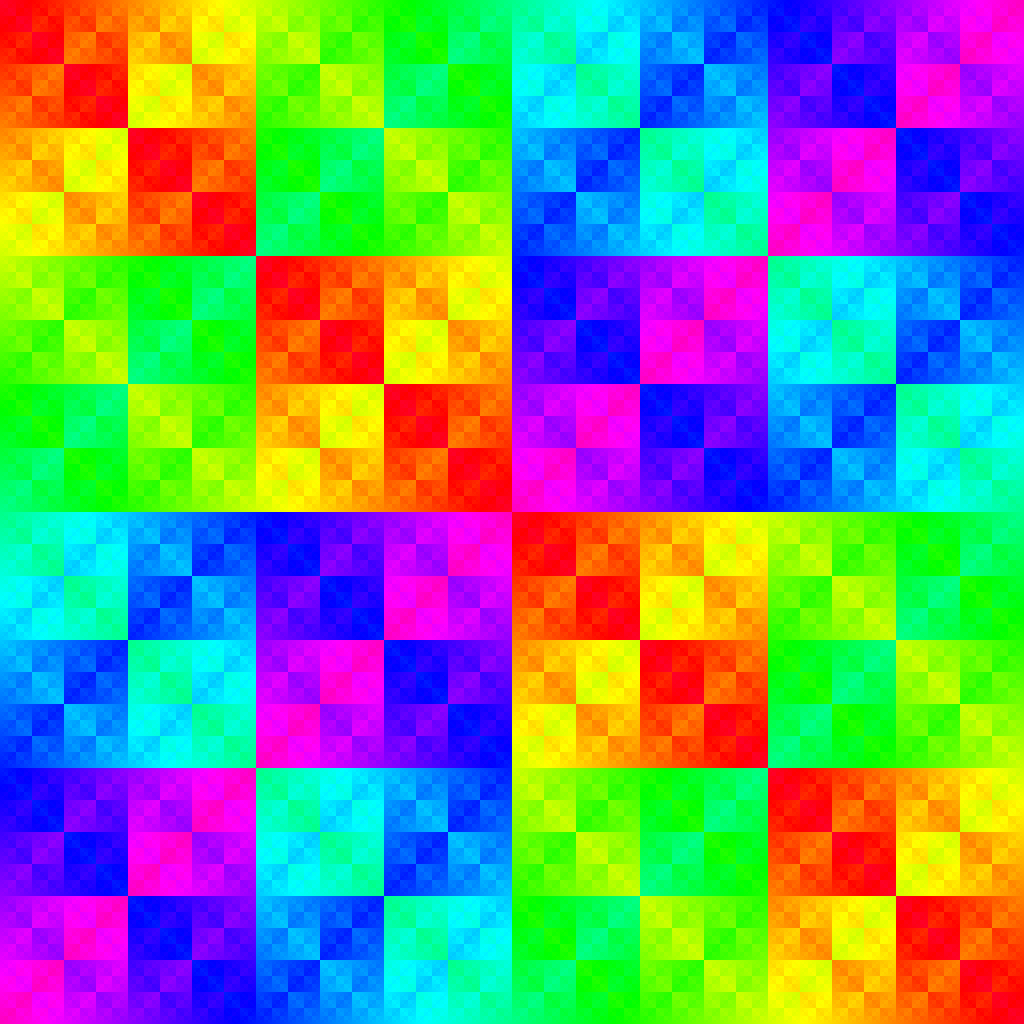The Cayley table of \(\mathbb{F}_2^n\) represents identifications in the Cayley graph of a Boolean function.

A Sidon set \(S\) in \(\mathbb{F}_2^n\) is a set such that the pairwise sums of distinct points are all distinct. The exclude points of a Sidon set \(S\) are the sums of three distinct points in \(S\), and the exclude multiplicity of a point in \(\mathbb{F}_2^n \setminus S\) is the number of such triples in \(S\) it is equal to. We call the function \(d_S \colon \mathbb{F}_2^n \setminus S \to \mathbb{Z}_{\geq 0}\) taking points in \(\mathbb{F}_2^n \setminus S\) to their exclude multiplicity the exclude distribution of \(S\). We say that \(d_S\) is uniform on \(\mathcal{P}\) if \(\mathcal{P}\) is an equally-sized partition \(\mathcal{P}\) of \(\mathbb{F}_2^n \setminus S\) such that \(d_S\) takes the same values an equal number of times on every element of \(\mathcal{P}\). In this paper, we use APN plateaued functions with all component functions unbalanced to construct Sidon sets \(S\) in \((\mathbb{F}_2^n)^2\) whose exclude distributions are uniform on natural partitions of \((\mathbb{F}_2^n)^2 \setminus S\) into \(2^n\) elements. We use this result and a result of Carlet to determine exactly what values the exclude distributions of the graphs of the Gold and Kasami functions take and how often they take these values.

Some Sidon sets such as this one have local repetition in their exclude points.

Let \(\mathbb{F}_p^n\) be the \(n\)-dimensional vector space over \(\mathbb{F}_p\). The graph \(\mathcal{G}_F = \{ (x, F(x)) : x \in \mathbb{F}_p^n \}\) of a vectorial function \(F \colon \mathbb{F}_p^n \to \mathbb{F}_p^m\) can have interesting combinatorial properties depending on varying cryptographic conditions on \(F\). A vectorial Boolean function \(F \colon \mathbb{F}_2^n \to \mathbb{F}_2^n\) is almost perfect nonlinear (APN) if there are at most \(2\) solutions to the equation \(F(x+a) + F(x) = b\) for all \(a,b \in \mathbb{F}_2^n\) where \(a \neq 0\). In this paper, we classify APN functions and important subclasses of APN functions in graph theoretical terms using the Kneser graph of all translations of \(\mathcal G_F\). We also study the properties of \(\mathcal G_F\) as a Sidon set. In particular, we introduce the notion of uniform exclude distributions, and we study APN functions whose graphs have uniform exclude distributions.

The adjacency matrix of \(\overline{Cay(\gamma_F)}\) where \(F(x)=x^3\) and \(n=4\).

A landmark result of Erdős, Ginzburg, and Ziv (EGZ) states that any sequence of \(2n-1\) elements in \(\mathbb{Z}/n\) contains a zero-sum subsequence of length \(n\). While algebraic techniques have predominated in deriving many deep generalizations of this theorem over the past sixty years, here we introduce topological approaches to zero- sum problems which have proven fruitful in other combinatorial contexts. Our main result is a topological criterion for determining when any \(\mathbb{Z}/n\)-coloring of an \(n\)-uniform hypergraph contains a zero-sum hyperedge. In addition to applications for Kneser hypergraphs, for complete hypergraphs our methods recover Olson’s generalization of the EGZ theorem for arbitrary finite groups. Furthermore, we give a fractional generalization of the EGZ theorem with applications to balanced set families and provide a constrained EGZ theorem which imposes combinatorial restrictions on zero-sum sequences in the original result.

We define a cap in the affine geometry \(\mathrm{AG}(n,2)\) to be a subset in which any collection of \(4\) points is in general position. In this paper, we classify, up to affine equivalence, all caps in \(\mathrm{AG}(n,2)\) of size \(k \leq 9\). As a result, we obtain a complete characterization of caps in dimension \(n \leq 6\), in particular complete and maximal caps. Since the EvenQuads card deck is a model for \(\mathrm{AG}(6,2)\), as a consequence, we determine the probability that an arbitrary \(k\)-card layout contains a quad.

A standard EvenQuads deck of cards.